MEAN TIME BETWEEN FAILURE & RELIABILITY – ALLAYING THE MYTHS

Mean time between failure & reliability – allaying the myths – By Mark Willis, Head of IPS and Strategic Development

Introduction

Mean Time Between Failure (MTBF) is the source of significant emotion and heated discussion in the world of Reliability Engineering. At first sight, there appears to be little value in the term and, for reasons best known to themselves, capability managers and requirements setters seem fixated by it. MTBF together with Availability are two of the most used, yet least understood, terms in the acquisition arena. I will dedicate another thought piece to Availability soon.

The main question which comes to mind when discussing MTBF is: does knowing how often on average a system fails add any value to the support decision-making process, especially when a significant number of people using the MTBF figure do not fully understand how it is derived or, indeed, the failure process?
This article contains my thoughts on the use of MTBF and I welcome any additional thoughts that the readership may have.

Reliability

Reliability is defined to be the probability that a component or system will perform a required function for a given period when used under stated operating conditions [Ebeling]. Reliability is a time-based probability. It is a value between 0 and 0.9999 recurring, and reliability reduces as a function of time.

Reliability is associated with one of the common failure distributions: Normal; Lognormal; Weibull or Exponential; the most common of which is Exponential.

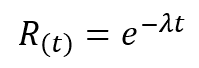
Where R(t) is Reliability at a given time and lambda is the failure rate.

The only relationship between reliability and MTBF is within this equation where lambda is the failure rate and MTBF is the inverse of the failure rate. So, let’s not get MTBF and Reliability confused – they are completely different. So much so that one of my erstwhile academic mentors would turn apoplectic if he heard both terms used in the same sentence.

Anecdote to reinforce the point:
Some 25 years ago I was in a meeting where a large OEM was trying to sell a digital automatic flying control system to me to replace an unreliable analogue version. The design engineer stated that the MTBF of the digital system was 2,400 hours against the analogue version’s 800 hours. Therefore, the engineer said, the digital system is three times as reliable. The engineer was taken aback when I told him that he did not know what he was talking about.

To explain to the novices – at zero operating hours, the equipment is equally reliable (0.9999) with the reliability curves beginning to diverge as the operating hours increase and reliability decreases. In this scenario, the three times as reliable point is not reached until around 1,500 operating hours and continues to diverge beyond that. However, for the engineer to state that the digital solution was three times as reliable showed that he did not understand reliability and Mean Time Between Falure .

Mean Time Between Falure (MTBF)

MTBF is what it says on the tin – it is a calculated mean. It is the mean time that one can expect between failures of a system or component when operated in a particular way. It assumes a constant failure rate throughout the life of the system – for obvious reasons, a dangerous assumption.

For a Normal failure distribution, MTBF is calculated by: Number of operations/Number of failures. This is the equation that you will see in several academic volumes but BEWARE.

Mechanical/Electronic/Electrical components do not fail ‘normally.’ The only things that can be accurately measured statistically using a Normal distribution are human beings – the Normal distribution is best suited to measure human behaviour with 95% of the population being within 3 standard deviations either side of the mean in a symmetrical bell curve distribution.

Most systems and components fail ‘exponentially.’ To calculate the MTBF for afailure distribution the manual mathematical process is as follows:

• Gather the failure data from at least 100 failures.
• Plot the data points on a range of distribution graph papers.
• Sketch the curves for the statistical population.
• Least square regress the curve to get a line of ‘best fit’.
• Undertake a Chi-squared and/or Kolmogorov-Smirnoff Test of Significance on the curve to prove it is not Lognormal.
• Drop a perpendicular line from 63% on the X-axis to cross the distribution and identify the MTBF.

There are, of course, software programs which will do all the above for you.

Why do we drop the line from 63% and not 50%? Because in an exponential scenario 63% of your equipment has failed by the time you achieve MTBF – a statistical phenomenon which tends to catch out suppliers when they are undertaking ranging and scaling.

From the mathematical process above it is not surprising that OEMs do not do MTBF calculations very well. That is also why we should treat any OEM MTBF data with suspicion. To get a good data population (statistical sample) you must test to obtain failure data from at least 100 failures – OEMs cannot afford to do this. So, what do they do? Most OEMs will use a standard MTBF sourced from Mil-Hdbk-217F Reliability Predictions of Electronic Equipment. Similar handbooks for mechanical equipment do exist but they are not as widely used.

So, where does this leave us:

• We need to be aware of where the OEM sourced their MTBF predictions.
• The 217F predictions are conservative and can be an order of magnitude out…
• …So, the use of ‘engineering judgement’ is acceptable if you know (or suspect) better.
• We must look at mechanical equipment in a different way.

Mechanical Equipment 

Mechanical Equipment is made up of many components put together in a larger component or system. Each of the components may subscribe to a Weibull failure distribution. A Weibull distribution has two key characteristics:

• The alpha characteristic (scale parameter) is an indication of the first failure (where the distribution crosses the x-axis for the first time).
• The beta characteristic (shape parameter) is an indicator of the failure mode (wear out, corrosion, tyre burst, bird strike etc) and controls the position on the x-axis of the second and future failures. Simply, a beta of 2.8 indicates wear out and a beta of 8 indicates corrosion, for example.

However, when one builds a system with component parts in the resultant reliability block diagram the shape parameter (beta) of the system Weibull mathematically tends towards unity…and a Weibull with a beta of 1.0 behaves in the same way as an Exponential distribution. Hence, my earlier assertion that most systems fail exponentially.

So, what does failing exponentially mean? The characteristics of exponential failures are that they are random in nature and cannot be predicted. That is why on components like engines and gearboxes there are secondary failure detectors like HUMS, Vibration Analysis and Wear Debris Analysis techniques used to assist in predictive or prognostic analysis.

Summary

• MTBF is a mean and equipment and systems are not averagely reliable.
• MTBF and Reliability are two different things.
• Calculating MTBF is not as straightforward as some people will have you believe.
• For statistical reasons most complex equipment fails exponentially (randomly).
• OEM MTBFs should be treated with caution.
• Mil-Hdbk-217F only provides predictions for electronic equipment.
• There is nothing wrong with using engineering judgement.